 The Voronoi implicit interface method
The Voronoi implicit interface method
Research Highlights
Selected examples — for a more comprehensive and up-to-date account, see preprints and list of publications.
Interfacial gauge methods
A myriad of fluid dynamics problems involve interface motion playing a crucial role in the global dynamics. Examples include bubble aeration, submersed vessel locomotion, peristaltic flow, ink jet dynamics, and crashing waves. Many of these problems can be effectively modelled with the incompressible Navier-Stokes equations, in which the domain and embedded interfaces change in time, with boundary conditions and interface jump conditions determined by forces like surface tension. In this Science Advances paper, I developed a class of methods, interfacial gauge methods, which faciliate high-order accurate solution of these equations. The methods use a type of "gauge freedom" to rewrite the Navier-Stokes equations in an alternative form, allowing one to design algorithms which reduce the numerical coupling between fluid velocity, pressure, and interface position. Consequently, artifacts such as "parasitic currents" and other typics of numerical boundary layers (which often plague low-order methods) do not arise, allowing one to precisely compute interfacial fluid dynamics. Interfacial gauge methods have been applied to two-phase flow driven by surface tension, rigid body fluid-structure interaction, free surface flow, and liquid atomisation dynamics.
A jet of water impacts on a reservoir of water underneath, forming ripples just above the surface as well as in the main jet. These ripples are caused by surface tension and are related to the Plateau-Rayleigh instability. (top) A rendering illustrating the results of a simulation studying this phenomenon, computed using interfacial gauge methods. (bottom) Plot of the fluid vorticity, revealing a type of vortex shedding that occurs at the base of the ripples not previously seen in experiment.
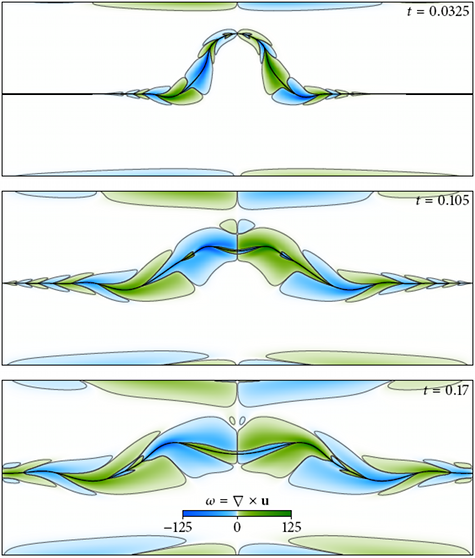
Capillary waves in surface tension dynamics [1]. Plots of fluid vorticity in incompressible fluid flow driven by surface tension reveal intricate "heart" shaped features. These are captured with high-order accuracy owing to the design of interfacial gauge methods.
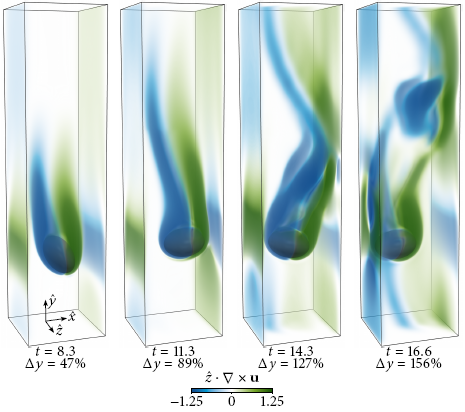
A falling tumbling rigid body submersed in a tall channel of liquid [1]. The figures show volume renderings of the outward-pointing component of vorticity, illustrating the onset of unsteady flow as the body tumbles over and oscillates from side to side.
Links
- New Mathematics Accurately Captures Liquids and Surfaces Moving in Synergy, Berkeley Lab Newscenter, 10 Jun 2016
 Multiscale modelling of foam dynamics
Multiscale modelling of foam dynamics Interfacial gauge methods
Interfacial gauge methods High-order accurate closest point calculation for implicitly defined surfaces
High-order accurate closest point calculation for implicitly defined surfaces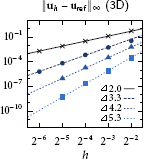 Implicit mesh discontinuous Galerkin methods
Implicit mesh discontinuous Galerkin methods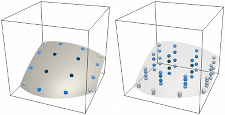 High-order accurate quadrature for implicitly defined domains
High-order accurate quadrature for implicitly defined domains