 The Voronoi implicit interface method
The Voronoi implicit interface method
Research Highlights
Selected examples — for a more comprehensive and up-to-date account, see preprints and list of publications.
High-order accurate quadrature for implicitly defined domains
An implicitly defined domain is either a volumetric region or codimension-one surface whose shape is characterised implicitly by an isosurface of a continuous scalar function. A variety of applications involving implicitly defined geometry require the evaluation of integrals over such domains, including level set methods for propagating interfaces in computational physics, embedded boundary methods for solving partial differential equations on curved domains, and in treating jump conditions and singular source terms in weak formulations. A specific example is that of implicit mesh discontinuous Galerkin methods, which has been developed to facilitate high-order accurate modelling of interfacial fluid dynamics.
In practice, to calculate integrals over implicitly defined domains, a quadrature scheme must be computed. The high-order accurate numerical quadrature algorithms I have developed are based on the idea of converting the implicitly defined geometry into the graph of an implicitly defined height function, and leads to a recursive algorithm on the number of spatial dimensions, requiring only one-dimensional root finding and simple one-dimensional Gaussian quadrature schemes. The resulting quadrature schemes have strictly positive quadrature weights and inherits the high-order accuracy of Gaussian quadrature, e.g., 20th order accuracy can be demonstrated. The resulting algorithms have been a key component in implicit mesh discontinuous Galerkin methods.
In the case of geometry defined implicitly via multivariate polynomials, the same techniques can be extended to handle even more complex geometry, including multi-component domains, high-curvature pieces, tunnels, junctions, self-intersections, and cusps.
For further details, including open-source C++ implementations, see here.
These algorithms have also been implemented in a variety of projects around the world, including LBNL's AMReX, LLNL's MFEM, deal.II, and BoSSS, as well as cutting edge research on immersed and extended finite element methods and cut cell finite volume methods in computational physics, chemistry, and materials.
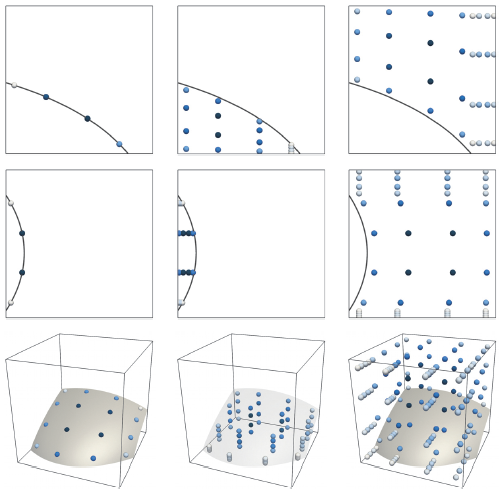
Some examples illustrating the quadrature schemes constructed by the algorithm (based on a one-dimensional Gaussian quadrature scheme of order 4) for surface integrals (left column) and volume integrals (middle/right columns) [1]. The weights are coloured according to a scale that is normalised for each particular case: pale indicates a low-valued weight and dark blue indicates a high-valued weight.
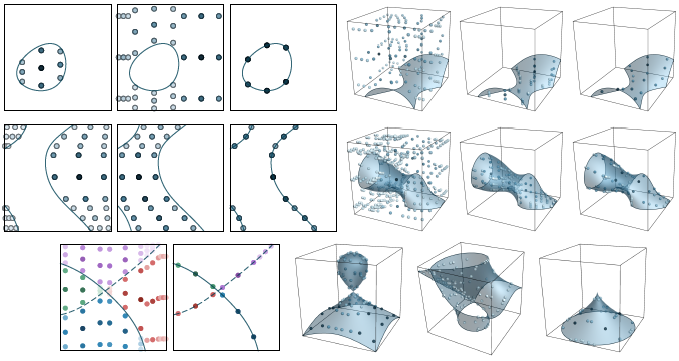
Some examples illustrating the quadrature schemes constructed by the algorithm (based on a one-dimensional Gaussian quadrature scheme of node-count 3) [2]. Each of the four examples in the top two rows illustrate the quadrature scheme for the inside, outside, and surface. The bottom-left example illustrates a case of two intersecting polynomials whose interfaces meet at a junction; the quadrature scheme is high-order accurate on each component (indicated by the colours). The bottom-right examples illustrate 3D cases with singularities, such as cusps and self-intersections.
References
- R. I. Saye, High-Order Quadrature Methods for Implicitly Defined Surfaces and Volumes in Hyperrectangles, SIAM Journal on Scientific Computing, 37(2), A993–A1019 (2015). Link pdf
- R. I. Saye, High-order quadrature on multi-component domains implicitly defined by multivariate polynomials, Journal of Computational Physics, 448, 110720 (2022). Link pdf
 Multiscale modelling of foam dynamics
Multiscale modelling of foam dynamics Interfacial gauge methods
Interfacial gauge methods High-order accurate closest point calculation for implicitly defined surfaces
High-order accurate closest point calculation for implicitly defined surfaces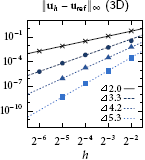 Implicit mesh discontinuous Galerkin methods
Implicit mesh discontinuous Galerkin methods High-order accurate quadrature for implicitly defined domains
High-order accurate quadrature for implicitly defined domains