 The Voronoi implicit interface method
The Voronoi implicit interface method
Research Highlights
Selected examples — for a more comprehensive and up-to-date account, see preprints and list of publications.
Implicit mesh discontinuous Galerkin methods
As part of my work on high-order accurate methods for interfacial fluid flow (see also interfacial gauge methods), I have been developing high-order accurate implicit mesh discontinuous Galerkin methods. The framework uses implicitly defined meshes (wherein a reference quadtree or octree grid is combined with an implicit representation of evolving interfaces and moving domain boundaries) to define a mesh with interface-conforming elements, allowing physically prescribed interfacial jump conditions to be captured with high-order accuracy. Many benefits arise from using such implicitly defined meshes: interface motion can be naturally coupled to the underlying physics; mathematical formulations, numerical discretisations and most geometric constructions can be cast independent of the spatial dimension; and, of particular interest in this work, interface dynamics, fluid dynamics, quadrature, etc., can all be made arbitrarily high-order accurate.
The framework can be used to solve scalar and vector-valued elliptic partial differential equations with interfacial jumps in rheological parameters, leading to optimal-order accuracy in the maximum norm, and discrete linear systems that are symmetric positive (semi)definite. Geometric multigrid methods have also been developed to efficiently solve these problems, and the framework has been coupled to dynamic implicit interface methods (such as the level set method and Voronoi implicit interface method).
The framework can be applied to, e.g., single phase flow in nontrivial geometry, surface tension-dirven two phase flow with phase-dependent fluid density and viscosity, rigid body fluid-structure interaction, and free surface flow. Convergence tests via the maximum norm show high-order accuracy for all cases in both 2D and 3D (the order of accuracy is a user-chosen parameter). Applications have included vortex shedding in nontrivial geometry, capillary wave dynamics revealing fine-scale flow features, falling rigid bodies tumbling in unsteady flow, free surface flow over submersed obstacles, high Reynolds number soap bubble oscillation dynamics, vortex shedding induced by the Plateau-Rayleigh instability, wave propoagation in elastic solids, and more recently, liquid atomisation dynamics.
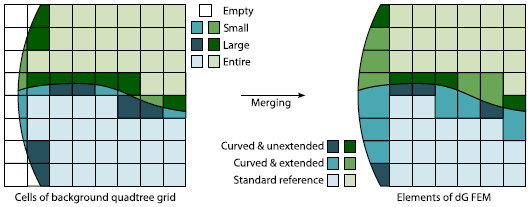
Schematic of an implicitly defined mesh [1]. (left) The cells of a Cartesian grid are classified according to whether they fall entirely within one phase ("entire", light blue/green and rectangular) or entirely outside the domain ("empty", white), or else are denoted "partial." Partial cells are classified according to whether they have a small volume fraction (medium shade blue/green) or large intersection (dark blue/green). (right) Small cells are merged with neighbouring cells in the same phase to form a finite element mesh composed of standard rectangular elements and elements with curved, implicitly defined boundaries.
References
- R. I. Saye, Interfacial gauge methods for incompressible fluid dynamics, Science Advances, 2(6), 1–14 (2016). Link pdf
- R. I. Saye, Implicit mesh discontinuous Galerkin methods and interfacial gauge methods for high-order accurate interface dynamics, with applications to surface tension dynamics, rigid body fluid-structure interaction, and free surface flow, Journal of Computational Physics
- and many others … see Publications.
 Multiscale modelling of foam dynamics
Multiscale modelling of foam dynamics Interfacial gauge methods
Interfacial gauge methods High-order accurate closest point calculation for implicitly defined surfaces
High-order accurate closest point calculation for implicitly defined surfaces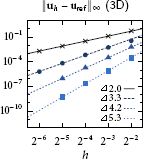 Implicit mesh discontinuous Galerkin methods
Implicit mesh discontinuous Galerkin methods High-order accurate quadrature for implicitly defined domains
High-order accurate quadrature for implicitly defined domains