 The Voronoi implicit interface method
The Voronoi implicit interface method
Research Highlights
Selected examples — for a more comprehensive and up-to-date account, see preprints and list of publications.
Multiscale modelling of foam dynamics
A foam consists of gas bubbles separated by thin liquid membranes called "lamellae"; these lamellae meet at junctions called "Plateau borders" that form a network of liquid tubes. Foam physics is extraordinarily complex and occurs over multiple scales in space and time. For example, a typical gas bubble may be millimetres to centimetres in size, whereas the lamellae are only micometres thick; individual films rupture in just milliseconds, bubbles rearrange in a small fraction of a second, and liquid inside the films drain (due to effects of gravity and surface tension) over tens of seconds or minutes.
To analyse the dynamics of foam as part of a computational model, it would be impractical to consider only the smallest space and time scales and let these determine the macroscale evolution, as this would require far too much computational power. In this Science article, we presented a numerical framework for modelling the multi-scale dynamics of a soap bubble foam. The work describes a method to separate distinct time and space scales and allow these to communicate in such a way that the most important physics affecting foam dynamics are captured. With the specification of external forces and different types of film liquid rheology, the model provides a computational framework for studying the interlinked effects of drainage, rupture, and rearrangement in a foam of bubbles. This work required development of efficient and robust mesh generators for finite element methods on moving curved interconnected surfaces, numerical methods for coupling adjacent lamellae and Plateau borders via flux boundary conditions, special-purpose time-integration methods for solving systems of fourth-order non-linear PDEs, and techniques to track and locally conserve liquid in stretching thin films.
Collapse of a cluster of bubbles under the combined effects of rearrangement, drainage, and rupture. A collection of soap bubbles initially in equilibrium undergoes liquid drainage in the thin films and Plateau borders, eventually causing one of the films to burst, instigating macroscopic rearrangement and overall collapse.

An example of a triangular mesh generated automatically from the Voronoi implicit interface method coupled to the multiscale foam model [1,2,3]. Individual lamellae are coloured differently and triangles meet consistently at junctions to form segmented line curves at Plateau borders. Triangulated meshes such as this one are used to solve for the fluid dynamics of liquid contained in the membranes via special kinds of thin-film equations.

Poster — The Life Cycle of a Bubble Cluster:
Insight from Mathematics, Algorithms, and Supercomputers (click for larger version)
References
- R. I. Saye and J. A. Sethian, Multiscale Modeling of Membrane Rearrangement, Drainage, and Rupture in Evolving Foams, Science, 340(6133), 720–724 (2013). Link pdf
- R. I. Saye and J. A. Sethian, Multiscale modelling of evolving foams, Journal of Computational Physics, 315, 273–301 (2016). Link pdf
- R. I. Saye, An algorithm to mesh interconnected surfaces via the Voronoi interface, Engineering with Computers, 31(1), 123–139 (2013). Link
 Multiscale modelling of foam dynamics
Multiscale modelling of foam dynamics Interfacial gauge methods
Interfacial gauge methods High-order accurate closest point calculation for implicitly defined surfaces
High-order accurate closest point calculation for implicitly defined surfaces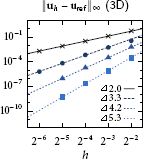 Implicit mesh discontinuous Galerkin methods
Implicit mesh discontinuous Galerkin methods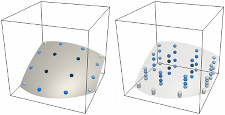 High-order accurate quadrature for implicitly defined domains
High-order accurate quadrature for implicitly defined domains