Research

My research interests are in mathematical modelling and scientific computation, particularly numerical methods for interfacial fluid dynamics, high-order accurate algorithms for implicitly defined geometry, and multi-scale and multi-physics simulation. Below are some examples of my work.

The Voronoi implicit interface method
Multiscale modelling of foam dynamics
Interfacial gauge methods
High-order accurate closest point calculation for implicitly defined surfaces
Implicit mesh discontinuous Galerkin methods
High-order accurate quadrature for implicitly defined domains

The Voronoi Implicit Interface Method

Many problems in science and engineering involve multiple interacting regions whose geometries change over time. The interfaces separating these different regions (or "phases") often meet at junctions and the physics taking place in the different regions can depend on a variety of factors, ranging from local geometry of the interface, to global properties transmitted instantaneously across the domain. A familiar example is the dynamics of a soap bubble foam in which gaseous bubbles are separated by a network of interconnected thin films of liquid. As bubbles rearrange in a foam due to effects of surface tension, gas dynamics, permeability, etc., the network of interfaces evolves in time, changing shape and connectivity.

In collaboration with James Sethian, I developed the Voronoi Implicit Interface Method for tracking multiple interacting and evolving regions whose motion may be determined by physics, jump conditions, internal constraints, geometric quantities, and boundary conditions. The method works in any number of spatial dimensions, accurately represents complex geometries involving triple and higher-order junctions, can be coupled to time-resolved physics, and automatically handles topological changes in the evolving interface, including creation and destruction of phases. The VIIM is an Eulerian-based method which represents the entire multiphase system with an unsigned distance function and region indicator function; these functions are evolved in time via implicit interface methods combined with a geometric construction based on the Voronoi diagram. Applications so far have included: multiphase mean curvature flow; advection; constant-normal-speed flows; coupling to incompressible multiphase fluid flow with variable density, viscosity and surface tension coefficients; problems on arbitrary-shaped domains; multi-region shape optimisation; image segmentation; and multi-scale modelling of bubble dynamics (see here).

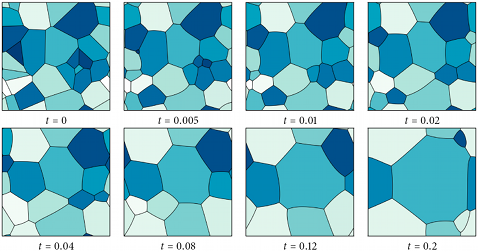
Curvature flow using the VIIM applied to an initial set of 25 randomly positioned phases. According to von Neumann-Mullins' law, phases with more than six sides grow, those with less than six shrink, and those with six sides conserve their area. This process leads to "coarsening" of the system [1,2].

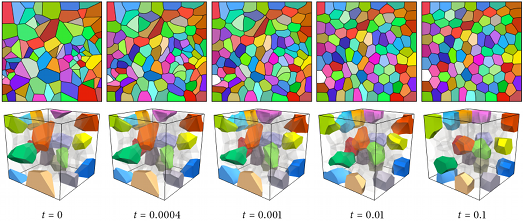
Mean curvature flow using the VIIM with area/volume targeting, so that every phase ultimately has the same area/volume [2]. (top) Two-dimensional example. (bottom) Three-dimensional example in which a selection of phases have been coloured solid.

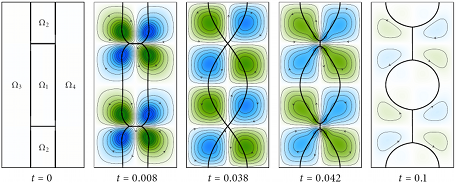
Coupling the VIIM to a four-phase fluid system which undergoes two T1 topological changes [2]. The contours show streamlines and the colours indicate the value of the stream function.

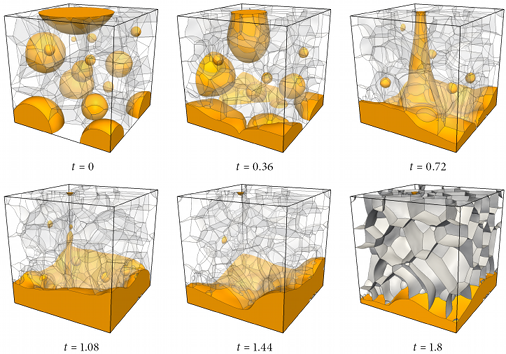
A multiphase simulation in which the VIIM is coupled to an incompressible Navier-Stokes solver in three dimensions with gravity, such that the orange coloured phase is more viscous and more dense than the other phases [2]. The bulk foam is rendered mostly transparent except for the last frame, where it is rendered opaque to make the structure clearer.

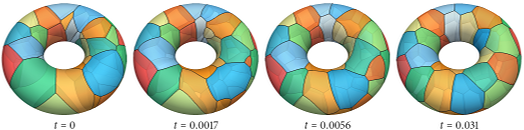
Applying the VIIM to mean curvature flow with volume targeting in a torus [3].

References

  1. R. I. Saye and J. A. Sethian, The Voronoi Implicit Interface Method for computing multiphase physics, Proceedings of the National Academy of Sciences, 108(49), 19498–19503 (2011). Link pdf
  2. R. I. Saye and J. A. Sethian, Analysis and applications of the Voronoi Implicit Interface Method, Journal of Computational Physics, 231(18), 6051–6085 (2012). Link pdf
  3. R. I. Saye, The Voronoi Implicit Interface Method with Applications to Multiphase Fluid Flow and Multiscale Modelling of Foam Dynamics, May 2013, University of California, Berkeley. Link pdf (52MB)