 The Voronoi implicit interface method
The Voronoi implicit interface method
Research Highlights
Selected examples — for a more comprehensive and up-to-date account, see preprints and list of publications.
High-order accurate closest point calculation for implicitly defined surfaces
A powerful technique for representing curves in two dimensions and surfaces in three dimensions is to define them implicitly, via a fixed isosurface/level set of a continuous scalar function. Implicit representations of surfaces lead to many mathematical and computational advantages in a variety of settings, such as in computing and manipulating surface geometry in interface tracking algorithms, solving partial differential equations on domains with moving boundaries and interfaces, and in computational geometry problems such as mesh generation.
Numerical methods making use of implicitly defined geometry often require accurate closest point calculations, e.g., in reinitialisation algorithms for level set methods, in evaluating Voronoi operators in the Voronoi implicit interface method, and to build smooth and accurate extension functions with prescribed values on a given implicitly defined surface. I have developed a set of high-order algorithms for closest point calculations for implicitly-defined codimension-one geometry; these algorithms are able to capture sub-grid details, can be used on unstructured meshes, and are made highly efficient via optimised k-d tree data structures. For further details, including open-source C++ implementations, see here.
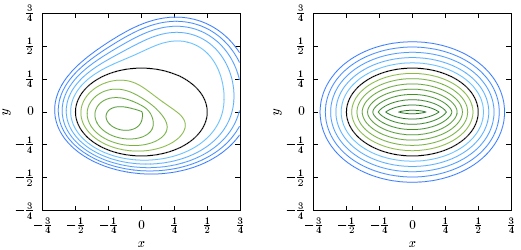
Reinitialising a two-dimensional level set function [1]. (left) Contour plot of a function which implicitly defines an elliptical interface (black curve). (right) Contour plot of the corresponding reinitialised signed distance function.

Level sets of a signed distance function reconstructed from the surface shown in grey [1]. This example was constructed from a small 5 by 5 by 5 patch of grid cells, in such a way that the droplet on the right is completely contained within one grid cell. Subgrid details such as this are important in high-order methods involving implicitly-defined geometry.
 Multiscale modelling of foam dynamics
Multiscale modelling of foam dynamics Interfacial gauge methods
Interfacial gauge methods High-order accurate closest point calculation for implicitly defined surfaces
High-order accurate closest point calculation for implicitly defined surfaces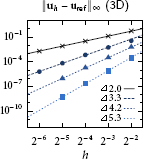 Implicit mesh discontinuous Galerkin methods
Implicit mesh discontinuous Galerkin methods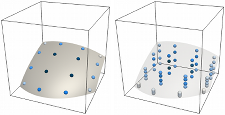 High-order accurate quadrature for implicitly defined domains
High-order accurate quadrature for implicitly defined domains